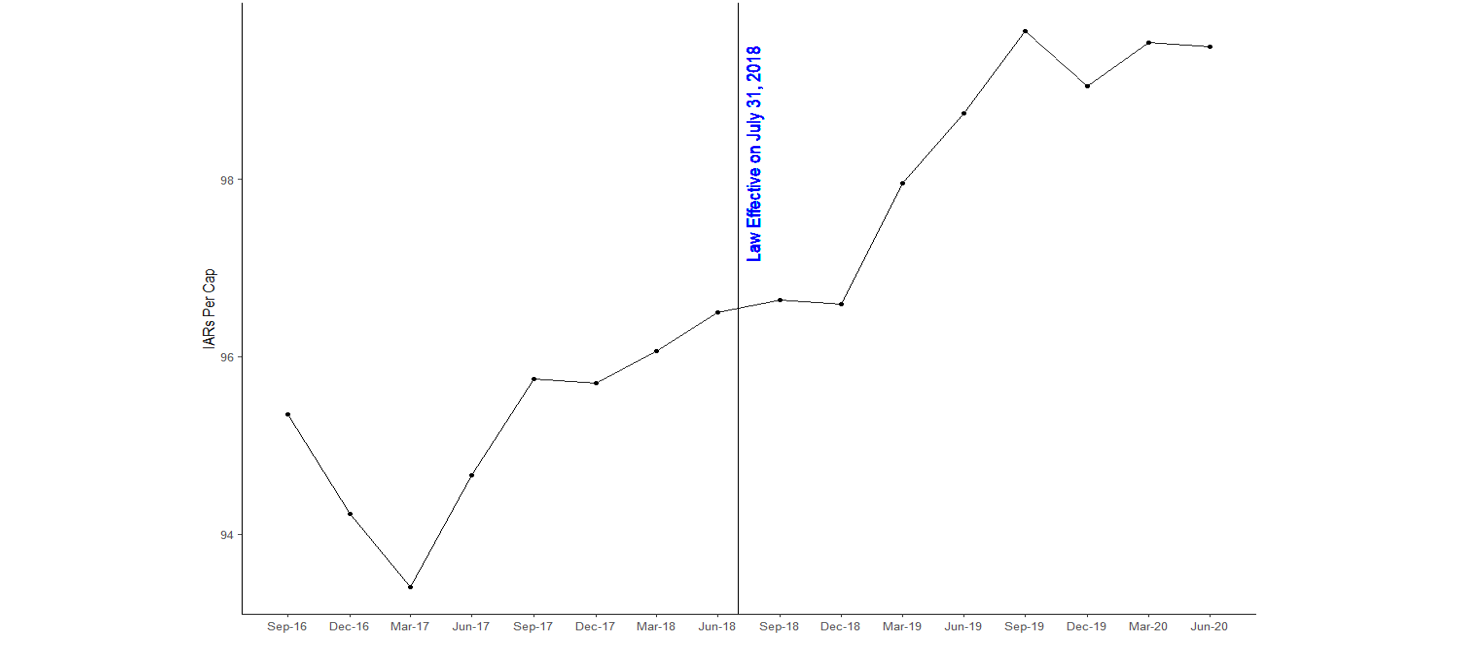
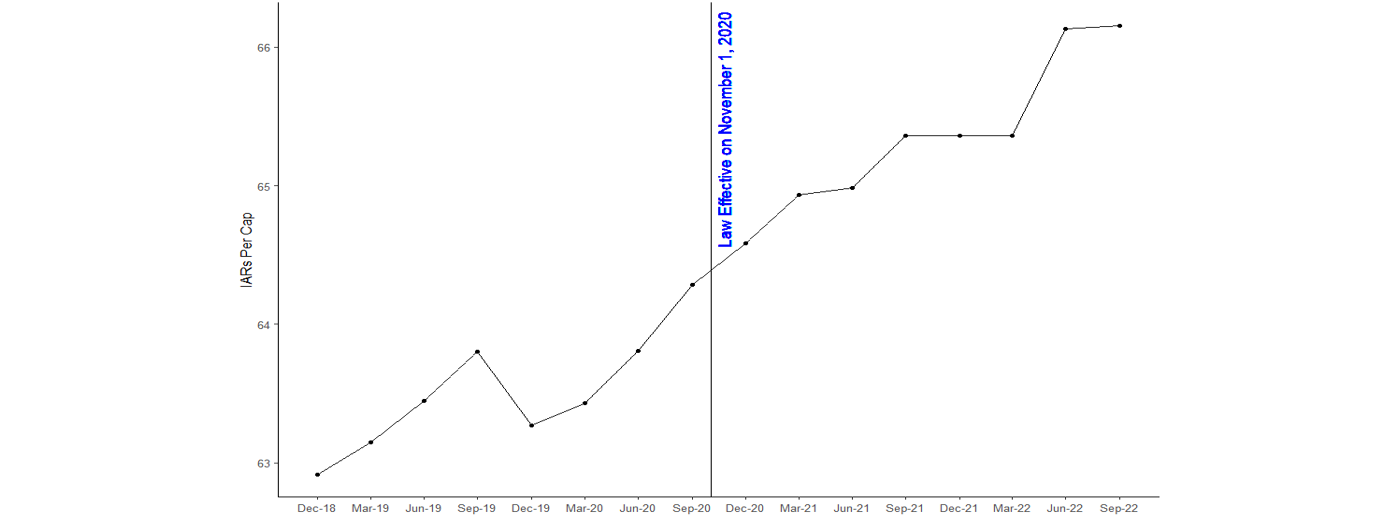
Aug 2024
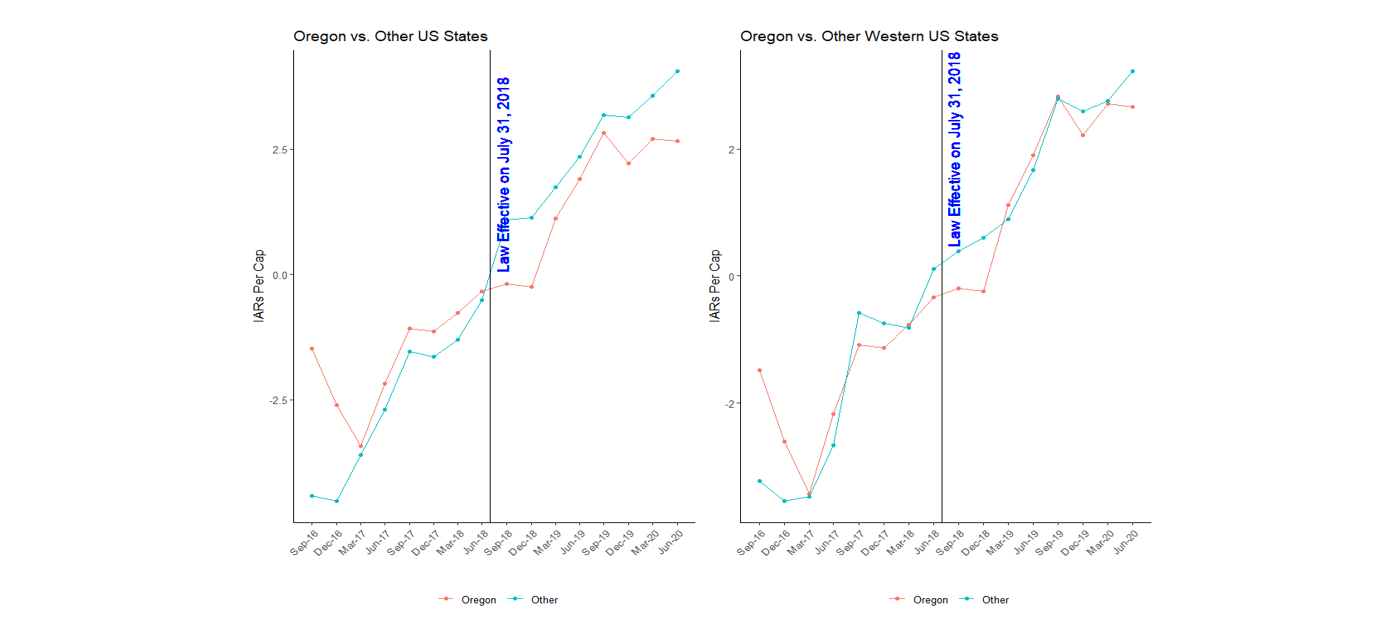
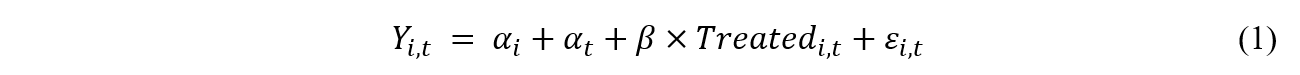
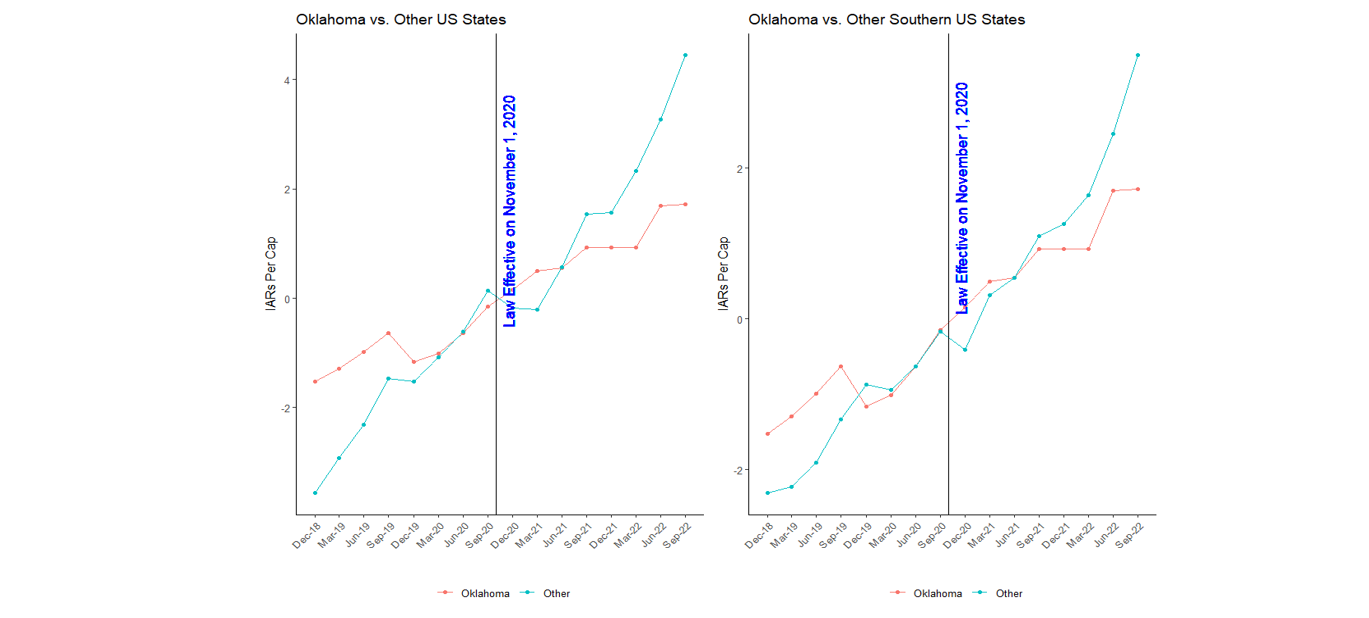
where \(Y_{i,t}\) is the number of IARs in state i in calendar quarter t, \(α_i\)are state dummy variables, \(α_t\) are calendar quarter dummy variables, \(Treated_{i,t}\) is an indicator equal to 1 when state i is Oregon and t is after July 31, 2018, and \(ε_{i,t}\) is a random error term. β is the parameter of interest and measures the effect of the E&O insurance law (treatment) on Oregon-registered IARs per cap. The sample used to estimate the regression includes all the state-quarter observations for all US states plus DC or all Western US states from March 31, 2017 through June 30, 2020, covering the 6 quarters before treatment where the parallel trends assumption is satisfied and 8 quarters after treatment.[6]
The estimate of β obtained using the control group of all other US states plus DC is equal to -1.30 with a standard error of 1.61. This negative estimate is statistically insignificant at any level, indicating that it may well be due to random chance. That is, the DID regression does not support the proposition that the Oregon law reduced access to investment advisory services. The estimated impact is economically as well as statistically small: 1.30 is equal to 1.2% of the overall sample average of the number of IARs per capita (107.6).
To further assess whether the β estimate provides evidence of a negative impact of the Oregon law, we estimate the DID regression 50 more times, each time on the subsample comprising 49 non-Oregon states and DC with a different state as the treated group. For each regression, we assume a hypothetical E&O insurance law became effective on July 31, 2018 in the respective state, while no such law went into effect in 2018 in any state other than Oregon. 29 of the 50 resulting estimates of the impact of the imaginary law are less than -1.30. That is, the β estimate for Oregon, despite being negative, is greater than the estimate of a nonexistent impact more than half of the time. This suggests that the estimate of -1.30 is probably due to chance and cannot substantiate any negative effect of the Oregon E&O insurance law on IAR registrations.
The β estimate based on the control group of all other Western US states is equal to -0.11 with a standard error or 0.90. The estimate is not only statistically insignificant at any level but also economically negligible: 0.11 is merely 0.1% of the overall sample average of the number of IARs per capita (93.3). Among the 12 DID regressions estimated on the sample including 12 non-Oregon Western US states each of which assumes a different treated state, 8 produce a β estimate less than -0.11. This indicates that the negative estimate of -0.11 for Oregon is likely due to chance, and there is no evidence that the Oregon law has a negative impact on IAR registrations.